- Digital Technologies Institute PTY LTD
- Sep 1, 2021
- 1 min read
Toowoomba is hosting the 2021 Queensland Society for IT in Education State Conference in the September school holidays on Sept 20+21. Check out the website which contains all the details of the two days Digital Tech + Digital Literacy conference, including keynote speakers, workshops, presentations, technology playground and the retro themed conference dinner to celebrate the 30th anniversary of QSITE and 40 years since the inception of the Computer Education Group of Queensland.
At the time of this blog post, Toowoomba is not in a lockdown zone. In this time of uncertainty with lockdowns and COVID, QSITE assures that if the conference is cancelled for any reason you will receive a full refund of your registration cost. Check with your accommodation provider before booking that they will also refund if you are unable to attend.
Start your school holidays off by visiting the garden city of Toowoomba and joining your colleagues in two days of highly engaging activities facilitated by experts from across Queensland.
Visit the website for all the details or contact office@qsite.edu.au for further information.


QSITE and the Digital Technologies Institute, supported by Google Australia, are conducting an introductory-level workshop on Artificial Intelligence at the Sunshine Coast.

Who should attend?
Late primary, secondary and pre-service teachers looking to take their first steps in artificial intelligence.
When and where?
Date: 23rd October 2021
Venue: Mountain Creek State High School, 100 Lady Musgrave Drive, Mountain Creek, QLD, 4557
The workshop runs from 9am - 3:00pm
What does it cost?
Because of funding from Google Australia, we can provide the event free of charge.
What does the workshop include?
The workshop provides a hands-on focus on artificial intelligence and machine learning. Participants obtain an introductory level understanding of AI and can recreate the curriculum-aligned activities in a classroom with students. There will be tons of hands-on activities and lesson plans, and we will keep tech jargon to a minimum. Don’t be afraid: You don’t need to be coding Ninja. Non-coders will be able to follow the entire workshop with ease.
Where can I register?
To register, go to https://qsite.edu.au/event/ai-workshop-qsite-sunshine-coast/
I have questions. Whom can I contact?
Email us here
We look forward to seeing you at the workshop.
- Jonas Schulz
- Aug 5, 2021
- 2 min read
In the past year we have been working extensively on the MyComputerBrain platform, adding new courses, improving the look of the website and overhauling the behind the scenes. So what have we done during this time? Here is a small overview.
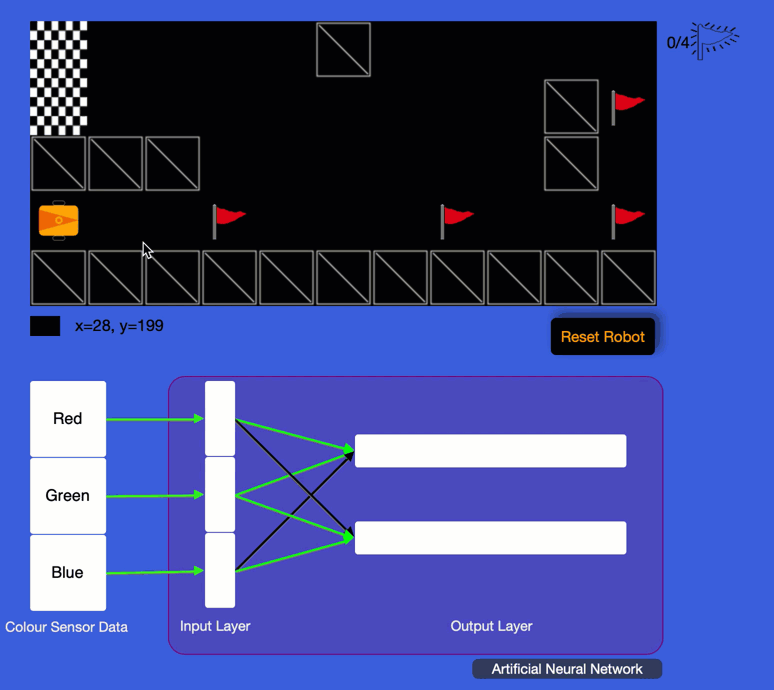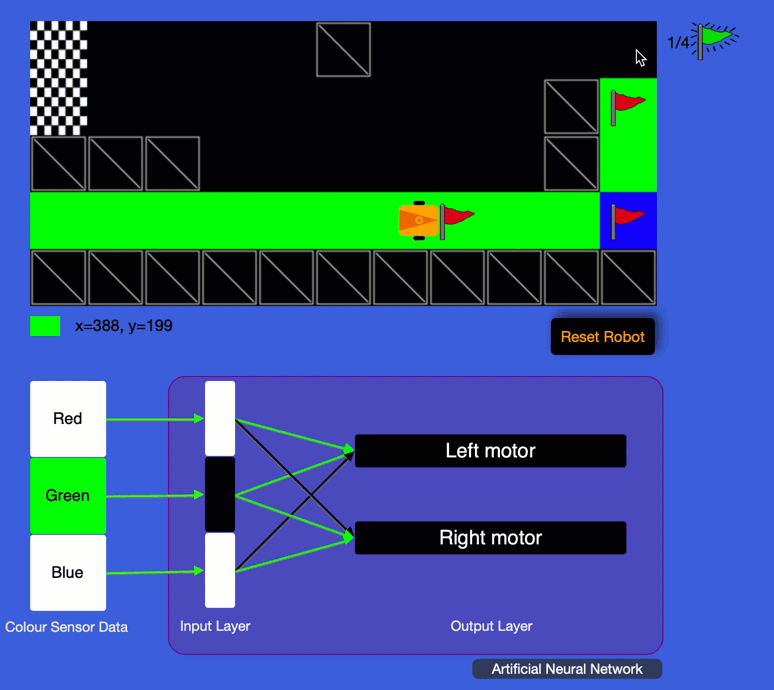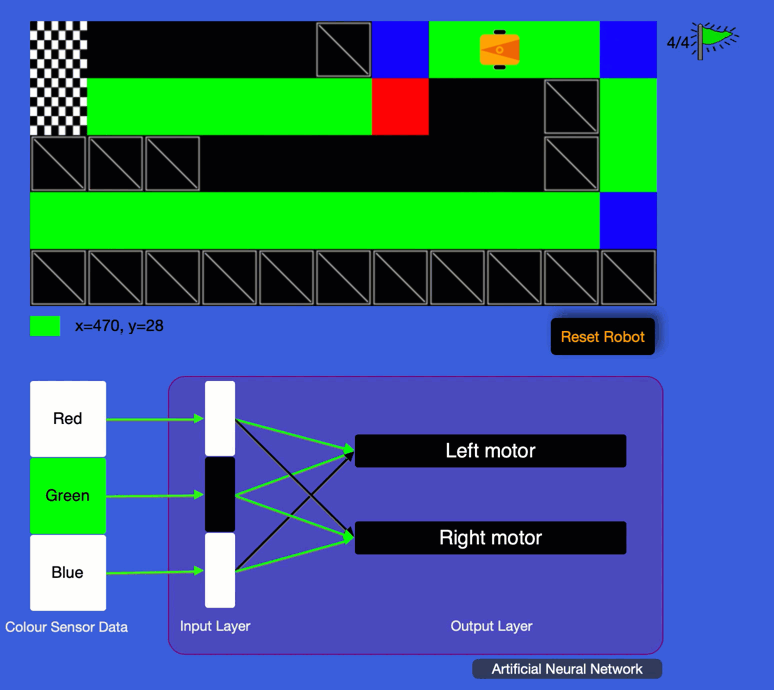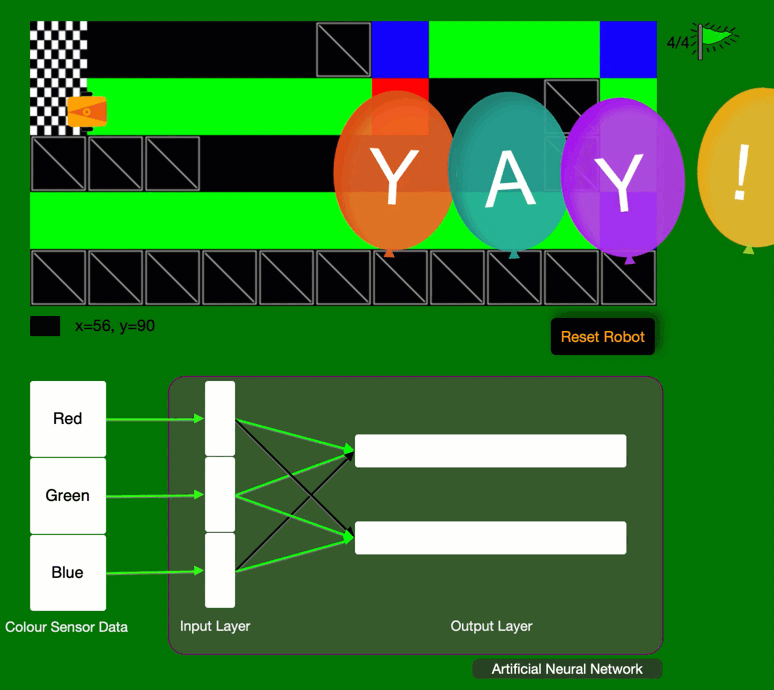
First off, welcome to our AI and Robotics course. which is our latest creation at the intersection of Artificial Intelligence and robotics and an interactive and easy first step into the amazing world of AI.
AI and Robotics Course
Who is the course for: Late primary and early secondary.
How many lessons: 18.
What does it teach: Artificial Intelligence, Machine learning and Data Representation.
Two New Videos
The next time you visit MyComputerBrain you might notice that we have added two new videos at the bottom of the home page. These videos are free learning tools from the Digital Technologies Hub that we had the privilege to contribute to.


Courses List
You may also notice that we have removed many of the courses from our home page. Instead, you'll be able find a list of all courses by navigating to our Courses page through the toolbar.
Here you will be able to view all the courses and import information including: a short description, the amount of lessons included in each course and the intended year group.
To purchase student accounts for the courses, visit the shop.
Teacher Portal
We have also been working on upgrading the teacher portal. Our aim is to make it as easy as possible for you to view the progress of your students as they progress through the courses.
This includes a new "Student Progress" tab on the "Teacher Account" page (must be logged in as a teacher).

Here you will be able to see where students are up to in their course, if they are stuck and access course certificates.
As you may have noticed, the student's name is currently their username. If you have set the student's name in the "My Students" tab (by entering the information in the table and clicking "Save"), the student's name will instead appear.

Charts
You may have noticed that we sometimes use charts in our lessons, such as in the AI Scientist lesson. Going forward, we have updated these charts, made them interactive and look a lot sleeker if you ask me.

And much, much more!
We have made many other changes, including:
Updating the toolbar and making it easier to use.
Adding prices to our home page.
Student certificates for courses.
General site improvements.
That's all for this update. See you next time!
.png)